The Role of Energy Modulation in Cosmic Equilibrium: Insights from MAM and the GC

Cosmic equilibrium is governed by the delicate interplay of energy flows and resonant interactions. This article examines how energy modulation—conceptualized within the Grand Containment (GC) framework and analyzed through Multidimensional Harmonic Mathematics (MAM)—can maintain equilibrium in complex physical systems, from gravitational waves to large-scale cosmic structures.

Energy Modulation and Resonance

In our framework, energy is not uniformly distributed but modulated by harmonic resonances. A key idea is that energy conservation in resonant systems is expressed through a dynamic balance:

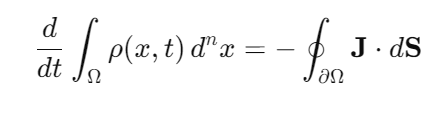
Here, p (x,t) represents the energy density, and J the energy flux. In the GC model, resonances create zones where energy is amplified or damped, leading to:

• Resonance peaks that drive rapid energy transfer.
• Damping regions where energy dissipates gently, stabilizing the system.

The modulation by the Fundamental Cosmic Frequency (FCF) can be integrated into the standard wave equation for gravitational perturbations:

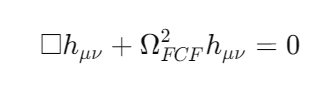
This additional term implies that the energy and phase of gravitational waves—and by extension, other cosmic phenomena—are subject to subtle, resonance-induced modulations.

Implications for Cosmic Equilibrium

Energy modulation through harmonic resonance offers new insights:

• It provides a mechanism for maintaining stability in dynamic systems.
• It suggests that cosmic evolution may be driven by oscillatory energy exchanges rather than monotonic processes.
• It opens pathways to understand phenomena such as the balance between expansion and contraction in the universe, or the energy fluctuations observed in gravitational wave data.

Conclusion

The integration of energy modulation into the framework of MAM and the GC represents a powerful tool for explaining cosmic equilibrium. By analyzing how resonances shape energy distributions, we can gain deeper insights into the self-regulating mechanisms of the universe. This approach paves the way for future theoretical and experimental studies, offering a unified view of energy transfer in both local and cosmological systems.