
Understanding the universe’s complex structure requires new mathematical lenses. In this article, we explore how harmonic resonance—when viewed through the framework of Multidimensional Harmonic Mathematics (MAM)—exhibits fractal dynamics across multiple scales. These dynamics suggest that resonant patterns are not isolated phenomena; they repeat and interconnect in a fractal-like manner, from microscopic interactions up to the structure of galaxies and clusters.
Fractal Resonance Dynamics
Harmonic resonance can be thought of as a process in which oscillatory components couple across different scales. In a fractal framework, the same resonant behavior appears at multiple levels. One can express this notion with a simplified relationship:
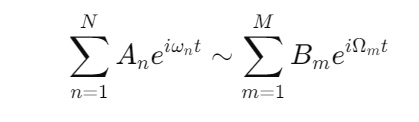
where the equality holds when resonant conditions repeat at different scales. In fractal systems, self-similarity implies that if a resonance pattern R(x)R(x)R(x) is observed at a small scale, a similar pattern emerges at a larger scale:
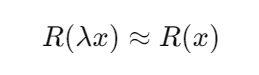
for a scaling factor λ. This self-similarity is the hallmark of fractal dynamics in harmonic interactions.
In cosmology, such fractal behavior could explain:
The fractal dynamics of harmonic resonance offer a promising avenue for understanding the self-similar nature of the universe. By applying MAM, we uncover patterns that may bridge micro and macro phenomena, providing a fresh perspective on cosmic organization. Future studies and simulations will help quantify these relationships and test their implications in observational cosmology.